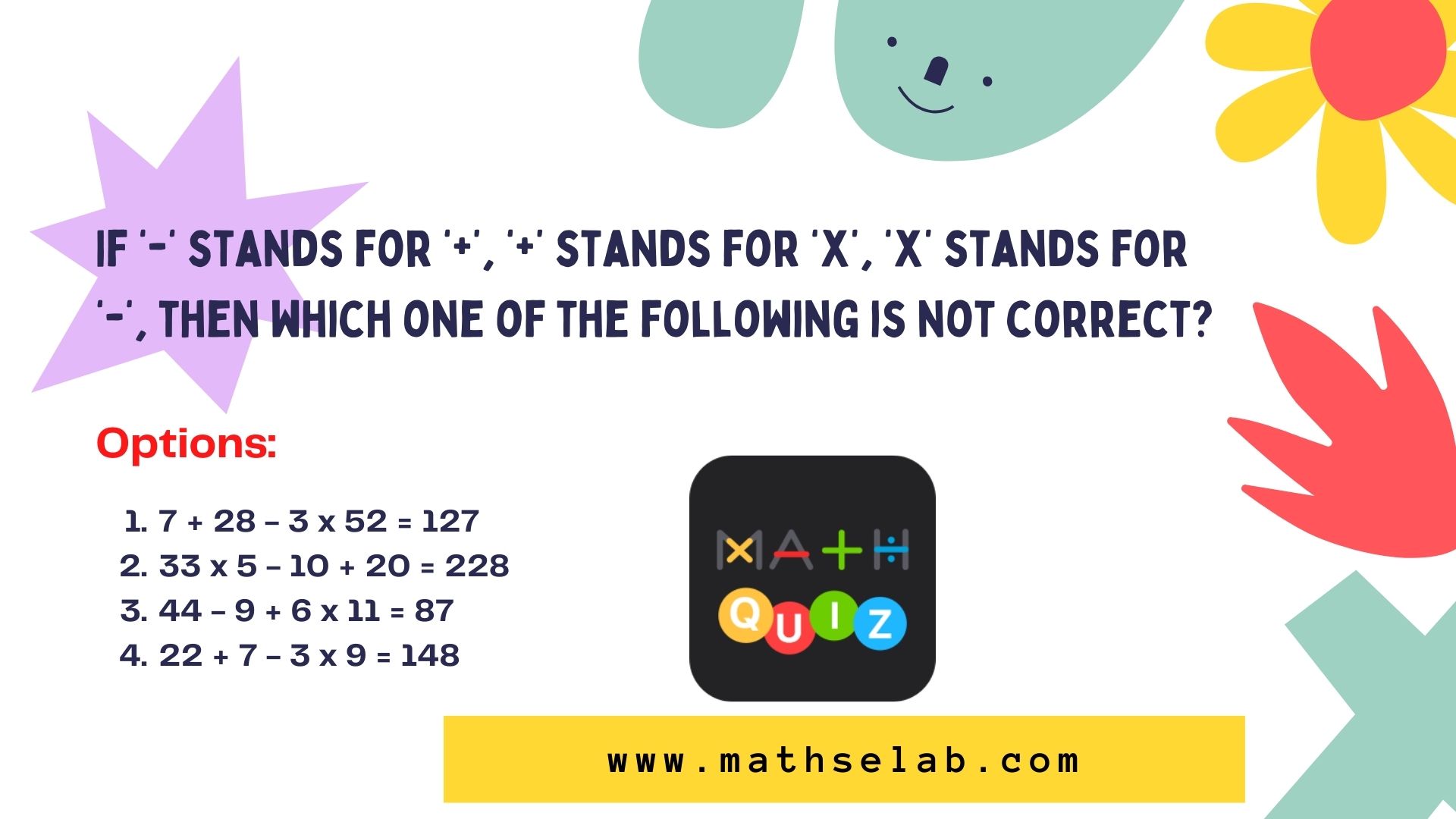Question
Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
A. 25200
B. 210
C. 24400
D. 21300
Answer: A
Solution:
Number of ways of selecting 3 consonants from 7 = 7C3
Number of ways of selecting 2 vowels from 4 = 4C2
Number of ways of selecting 3 consonants from 7 and 2 vowels from 4 = 7C3 × 4C2
= (7 × 6 × 53 × 2 × 1) × (4 × 32 × 1) = 210
It means we can have 210 groups where each group contains total of 5 letters (3 consonants and 2 vowels).
Number of ways of arranging 5 letters among themselves =5!
= 5 × 4 × 3 × 2 × 1 = 120 =5!
= 5 × 4 × 3 × 2 × 1 =120
Hence, required number of ways = 210 × 120 = 25200