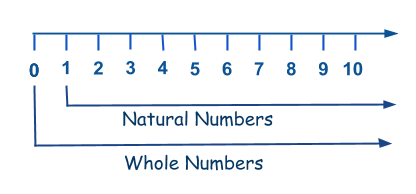
What are whole numbers?
Whole numbers are the set of numbers that include zero and all the natural numbers that we count with, like 0, 1, 2, 3, 4, 5, etc. What this set doesn’t cover are negative numbers and numbers that are communicate as fractions or decimals. In other words, whole numbers include zero and all positive integers. The set of whole numbers goes on forever.
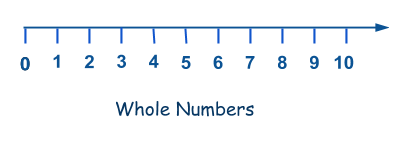
The number line above only shows whole numbers from 0 to 10. However, not all numbers are shown. 50 is also a whole number. Similarly, 2000 is also a whole number as the following figure shows.
Example: -2, -1, 0, 1, 2, 1/3, 0.232
Answer:
-2 and -1 are negative numbers, so they are not whole numbers.
0, 1, and 2 are all whole numbers.
1/3 is not a whole number because it’s a fraction.
0.232 is not a whole number because it’s a decimal.
Even and Odd Numbers
All whole numbers except for zero can be described as either even or odd.
Even number:- A number is called “even” if it can be divided by 2 with no remainder. Since 6 ÷ 2 = 3, the number 6 is an even number. In fact, all numbers that end in 0, 2, 4, 6, and 8 are even numbers.
Odd numbers :- Odd numbers are not divisible by 2. If we try to divide 3 by 2, for example, we get a quotient of 2 with a remainder of 1. All numbers that end in 1, 3, 5, 7, and 9 are odd numbers.
Challenge: Look at the following numbers and decide which ones are odd and which ones are even.
14, 18, 26, 31, 44, 51, 63, 74, 88, 91, 95, 100
Answer: By looking at the last digit of each number, we can determine that 14, 18, 26, 44, 74, 88 and 100 are even, while 31,51, 63, 91 and 95 are odd.
Basic Operations With Even And Odd Whole Numbers
It’s helpful to remember a few rules for the way odd and even numbers work together in equations.
The Addition rules
Addition rule 1: Even + Even = Even (Example: 4 + 2 = 6)
Addition rule 2: Even + Odd = Odd (Example: 1 + 6 = 7)
Addition rule 3: Odd + Odd = Even (Example: 9 + 5 = 14)
The subtraction rules mirror the addition rules
Subtraction rule 1: Even – Even = Even (Example: 6 – 4 = 2)
Subtraction rule 2: Even – Odd = Odd (Example: 6 – 3 = 3)
Subtraction rule 3: Odd – Odd = Even (Example: 9 – 5 = 4)
The multiplication rules are a little different
Multiplication rule 1: Even x Even = Even (Example: 4 x 4 = 16)
Multiplication rule 2: Even x Odd = Even (Example: 4 x 1 = 4)
Multiplication rule 3: Odd x Odd = Odd (Example: 5 x 7 = 35)
Note:- There are no division rules for even and odd numbers.