What is Real Numbers ?
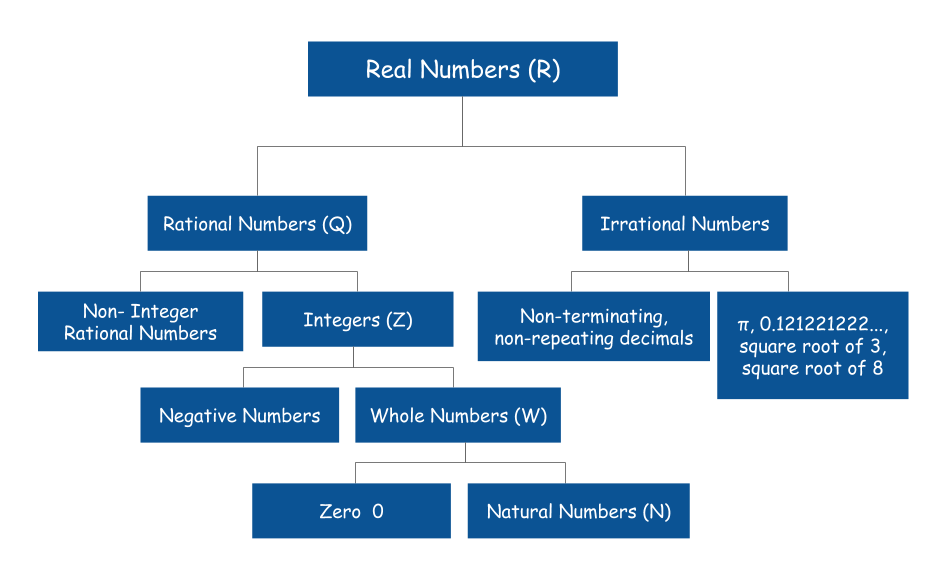
Real numbers are simply the combination of rational and irrational numbers, in the number system. They can be both positive or negative and are signify by the symbol “R”. All the natural numbers, decimals, and fractions come under this category.

Set of Real Numbers
The set of real numbers consist of different categories, such as natural and whole numbers, rational and irrational numbers and integers.
In the table given here, all these numbers are defined with examples.
| Category | Definition | Example |
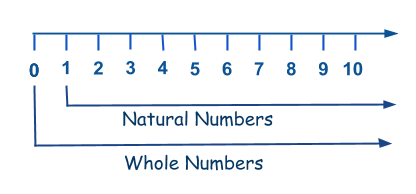
| Natural Numbers | Contain all counting numbers which start from 1. N = {1,2,3,4,……} | All numbers such as 1, 2, 3, 4,5,6,…..… |
| Whole Numbers | Collection of zero and natural number. W = {0,1,2,3,…..} | All numbers including 0 such as 0, 1, 2, 3, 4,5,6,…..… |
| Integers | The collective result of whole numbers and negative of all natural numbers. | Includes: -infinity (-∞),……..-4, -3, -2, -1, 0, 1, 2, 3, 4, ……+infinity (+∞) |
| Rational Numbers | Numbers that can be written in the form of p/q, where q≠0. | Examples of rational numbers are ½, 5/4 and 12/6 etc. |
| Irrational Numbers | All the numbers which are not rational and cannot be written in the form of p/q. | Irrational numbers are non-terminating and non-repeating in nature like √2 |
Real Numbers Chart
Properties of Real Numbers
There are four main properties which include commutative property, associative property, distributive property, and identity property. Consider “p, q and r” are the real numbers. Then based on these properties, we can define the numbers as;
Commutative Property
If p and q are the numbers, then the general form will be p + q = q + p for addition and p.q = q.p for multiplication.
Addition: p + q = q + p.
For example, 5 + 3 = 3 + 5, 2 + 4 = 4 + 2
Multiplication: p × q = q × p.
For example, 5 × 3 = 3 × 5, 2 × 4 = 4 × 2
Associative Property
If p, q and r are the numbers. The general form will be p + (q + r) = (p + q) + r for addition(pq) r = p (qr) for multiplication.
Addition: p + (q + r) = (p + q) + r.
An example of additive associative property is 10 + (3 + 2) = (10 + 3) + 2.
Multiplication: (pq) r = p (qr).
An example of a multiplicative associative property is (2 × 3) 4 = 2 (3 × 4).
Distributive Property
For three numbers p, q and r, which are real in nature, the distributive property is in the form of :
p (q + r) = pq + pr and (p + q) r = pr + qr.
Example of distributive property is: 5(2 + 3) = 5 × 2 + 5 × 3. Here, both sides will yield 25.
Identity Property
There are additive and multiplicative identities.
Addition: p + 0 = p. (zero is additive identity)
Multiplication: a × 1 = 1 × a = a. (1 is multiplicative identity)