A rectangle has a length that is 3 meters more than its width. If the perimeter is 24 meters, find the length and width of the rectangle.

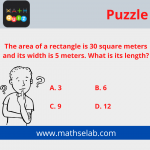
A rectangle has a length that is 3 meters more than its width. If the perimeter is 24 meters, find the length and width of the rectangle.

(A) 8 m, 5 m

(B) 7.5 m, 4.5 m

(C) 10 m, 7 m

(D) 11.5 m, 8.5 m

Answer: (B) 7.5 m, 4.5 m

Solution:

Let’s denote the width of the rectangle as w meters. Since the length is 3 meters more than the width, the length is w + 3 meters.

The formula for the perimeter (P) of a rectangle is given by:

P = 2 × (Length + Width)

In this case, the perimeter is given as 24 meters, so we can set up the equation:

24 = 2 × (w + (w + 3))

Now, let’s solve for w:

24 = 2 × (2w + 3)

Distribute the 2:

24 = 4w + 6

Subtract 6 from both sides:

18 = 4w

Divide by 4:

w = 18/4

w=4.5

So, the width (w) is 4.5 meters. Now, we can find the length:

Length = w + 3

Length = 4.5 + 3

Length = 7.5

Therefore, the length of the rectangle is 7.5 meters, and the width is 4.5 meters.