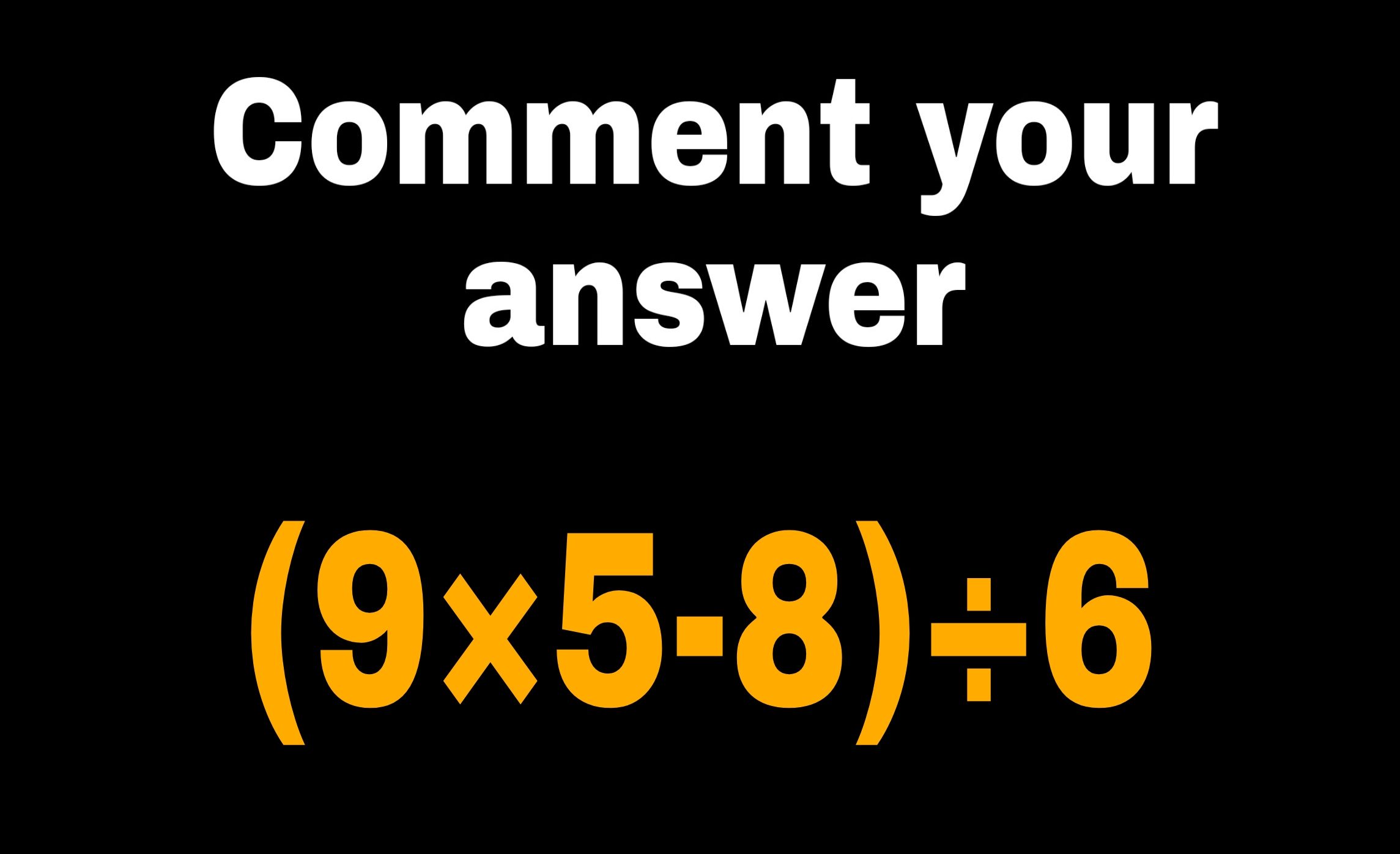Question
Which term of the series 5, 8, 11, 14, …. is 320
A. 65th
B. 107th
C. 105th
D. 106th
Answer: D. 106th
Solution:
Clearly, 5 + 3 = 8, 8 + 3 = 11, 11 + 3 = 14, …
So, the series is an A.P. in which a = 5 and d = 3.
Let 320 be the nth term of the series.
Then, 320 = 5 + (n – 1) × 3
=> (n – 1) = 105
=> n = 106.
Read more:
| If a + b = 3 and a^2 + b^2 = 7, what is a^4 + b^4? | In the series 3, 9, 15, ….. what will be the 21st term? |
| Which number is missing from this? | Evaluate: -18 + 4(6 ÷ 2)^2 |