Question
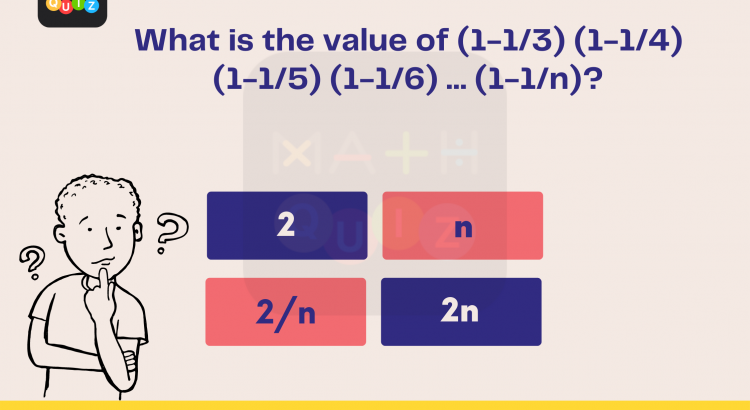
What is the value of (1-1/3) (1-1/4) (1-1/5) (1-1/6) … (1-1/n)?
A. 2
B. n
C. 2/n
D. 2n
Answer: C. 2/n
Solution:
Given series is
(1-1/3) (1-1/4) (1-1/5) (1-1/6) … (1-1/n)
= 2/3 × 3/4 × 4/5 × 5/6 × ⋯ × (n−2)/(n−1) × (n−1) / n
=2/n
Hence, the series
(1-1/3) (1-1/4) (1-1/5) (1-1/6) … (1-1/n) = 2/n .