Question
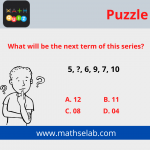
The sum of the series 5 + 9 + 13 + … + 49 is:
A. 351
B. 535
C. 435
D. 324
Answer: D. 324
Solution:
The given series is 5 + 9 + 13 + … + 49
which is an arithmetic progression with first term a = 5 and common difference d = 4.
Let’s say that the last term 49 is the nth term.
∴ a + (n – 1)d = 49
⇒ 5 + 4(n – 1) = 49
⇒ 4(n – 1) = 44
⇒ n = 12.
And, the sum of this AP is:
S12 = ((First term + Second term) / 2) * 12
s12 = ((5 + 49) / 2) * 12
= 54 * 6
= 324.
Hence, The sum of the series 5 + 9 + 13 + … + 49 is: 324.
Read More:
How do I solve 1 + 3 + 5 + 7 +… + 101?
What is the value of 1 ÷ [1 + 1 ÷ {1 + 1 ÷ (1 + 1 ÷ 2)}] = ?
Related Posts:
