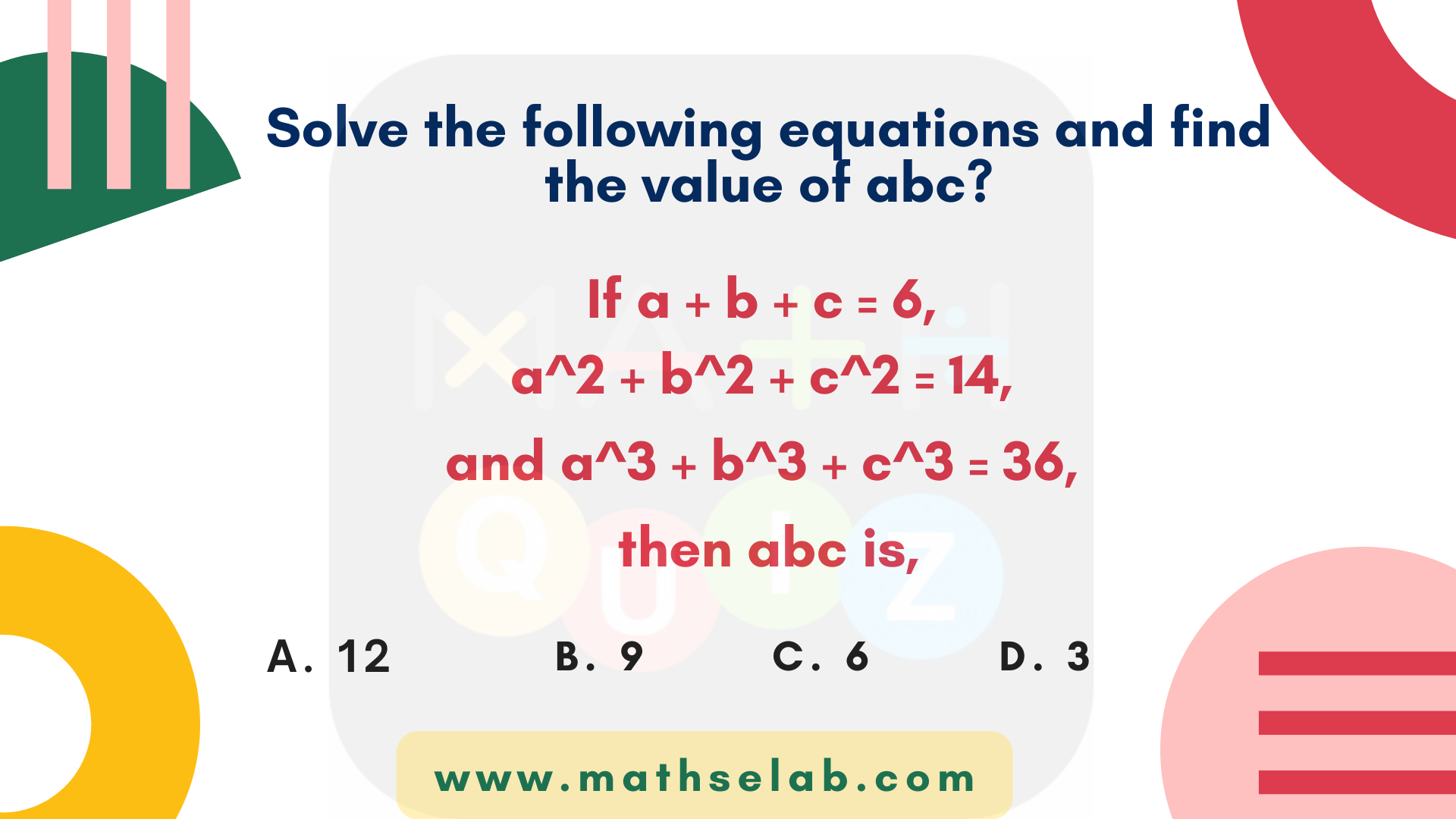Solve the following equations and find the value of abc? If a + b + c = 6, a^2 + b^2 + c^2 = 14, and a^3 + b^3 + c^3 = 36, then abc is,

Question

Solve the following equations and find the value of abc?

If a + b + c = 6, a² + b² + c² = 14, and a³ + b³ + c³ = 36, then abc is,

A. 12

B. 9

C. 6

D. 3

Answer: C. 6

Solution:

From the given equations,

(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)

=> (6)² = 14 + 2(ab + bc + ca)

=> 36 – 14 = 2(ab + bc + ca)

=> 22/2 = ab + bc + ca

=> ab + bc + ca = 11

a³ + b³ + c³ − 3abc = (a + b + c)(a² + b² + c² − ab − bc − ca)

= (6) (14 – 11)

= (6)(3)

= 18

Since, a³ + b³ + c³ − 3abc = 18

36 – 3abc = 18

-3abc = 18 – 36

-3abc = -18

abc = 6.

Read more:

If a^2 + b^2 + c^2 = 20 and a + b + c = 0, find ab + bc + ca.

If a + b = 12 , b + c = 17 and c + a = 11 what is the value of a + b + c?